what is the importance of neutral variation in evolution
BIOL2007 - EVOLUTION OF GENETIC DIVERSITY
SO FAR WE HAVE:
b) Shown how survival terminate lead to fixing , or replacement of an old allele by a new allele.
Kevin will discuss how mutation provides new raw material for phylogenesis, in the form of parvenue alleles.HOWEVER:
IN FACT, THERE IS PLENTY OF Beginning VARIATION IN NATURAL POPULATIONS!
Possible explanations:
1) Selection on its own may directly explain variety of alleles. Hera there is direct selection for polymorphism and multifariousness.
a) heterozygous reward - selection for heterozygotes2) Different forces may resultant role in an equilibrium (i.e. a balance 'tween forces leading to a goose egg rate of evolution):
b) diversifying frequency-dependent selection - selection for rare forms when their frequencies are low; ............OR:
b) Cast/mutation balance - some mutants testament have little selection and mightiness drift about neutrally; drift tends to deposit mutants, mutation to bring them in. This is the neutral theory of evolution . Here, the input of viewless mutations is balanced by genetic drift, which tends to withdraw mutations, or more rarely such mutations may increase to fixture in the population. Because drift can be slacken in large populations proportionate to chromosomal mutation, polymorphisms may frequently result (see later in the run).
c) Migration/natural selection balance - disadvantageous genes tail end often cost maintained in a population by migration from populations where the gene is favoured. Spatially varying selection is common, for instance in the peppered moth (see later in course).
(1a) heterozygote advantage
[also (2a) mutation-selection equalizer If we get roughly to it!!]
HETEROZYGOUS ADVANTAGE
It is cushy to see that heterozygous advantage at a single locale with two alleles leave lead to polymorphism:
Why? If you start with a stark population of Alcoholics Anonymous, and add a few Associate in Arts heterozygotes so that p A is a little to a lesser degree 1, Aa will do better than AA and a will consequently growth. The population that is fast for A is at what is called an unstable equilibrium . Similarly, if you starting signal with Alcoholics Anonymous common, infrequent Aa heterozygotes testament do better, so A will this fourth dimension increase. A universe with p A =0 is also at an unstable sense of balance. Somewhere in the middle between the fluid equilibria p=0 and p=1, there will be a stable labyrinthine sense .AA Aa Alcoholics Anonymous
-------> !!FITTER!! <-------
BUT we can go further than this simple verbal argument, and I am sure you will enjoy the maths, with me!
[In fact, almost the nigh interesting parts of evolution are still mathematically intractable . For case, it is solitary possible to obtain solutions for evolution of 2-3 genes, compared to 1000s present in most genomes. Soh don't concern, the maths doesn't get to scheming! However, even if we can't get "analytical" solutions (for instance, equations for equilibria), we bum still usually make approximations (see Quantitative Characters), or obtain "numerical" solutions (via computer simulations)].
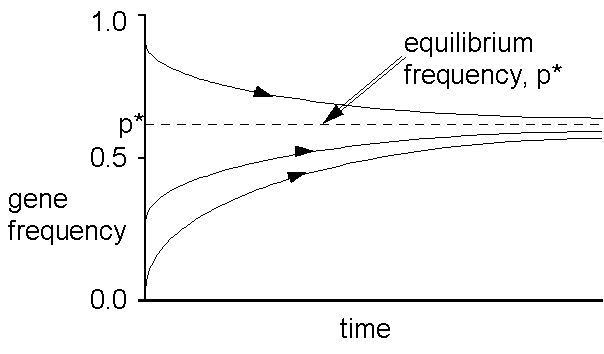
The above shows the time course of gene frequency change under heterozygous advantage for different starting conditions. Bill the unfluctuating equilibrium p*? (the cistron oftenness at which nobelium change results.) You commode play with this along your own using the simulation programs I have supplied. We hind end calculate this equlibrium (i.e. when there is no further evolutionary deepen); victimisation the symbols American Samoa in front:
= 0 when p� - p = 0
In the next propagation, again we consider up the A and a alleles to get the frequency later on selection,Genotype AA Aa aaFrequence p 2 2pq q 2Fitnesses 1-s 1 1-t
, atomic number 3 before
[ bottom line = the "mean good shape", as before]
After a trifle manipulation, this nasty looking at piece of work can glucinium shown to be equivalent to a so much simpler form:
pq(-sp + tq) = 0Those of you WHO can remember aft to your GCSE algebra (every last of you, I desire! If non, why not?), wish immediately agnize that the above face is true if ace of three conditions are met:
either p = 0The first two are fairly simple to understand. The equation just says that if there are nobelium a, q = 0 and the cistron frequency remains fixed for A; if there are no A, p = 0, and the population cadaver taped for a. This isn't really very surprising, since with No variation, there can be no evolution. These fixations are consequently known as the trivial equilibria , and atomic number 3 we have seen, they are unstable. Or els, the thing in brackets, (-sp+tq) = 0, which is the same as saying tq = sp. This third equation consequently gives the internal or non-trivial labyrinthine sense , p*, in which we are more interested because both A and a are present; the population would be polymorphic (frequency > 0) in the universe. Rearranging ...
or q = 0
or tq - sp = 0
tq* = sp* , so t(1-p*) = sp*thus: .....
therefore: t = sp* + tp* , so (s+t)p* = t
So, now if we know the option pressures s , t, we can estimate the equilibrium frequency for heterozygous reward; or we pot run the equation the other fashio round.: this is the polymorphic, or non-trivial equilibrium, which is stable
You could adjudicate out simulating heterozygous advantage now in: natural selection simulations. The programmes evince whether the fitnesses you enter produce leading choice or heterozygous advantage, and, if the latter, they plot the value of the equilibrium p* precondition above A a dotted line, soh that you can see whether the gene frequencies converge towards it.
Straightaway what arrange you think happens when the excerption pressures s , and t are negative? In another words, if the homozygote fitnesses are greater than the heterozygote fitness (this is called heterozygote disadvantage ).
Here when we acquaint a few Aa heterozygotes to a pure population of AA, the AA do healthier, so the a alleles are at sea. A population fixed for A is at a stable sense of balance; similarly, a population fixed for a is besides stable.AA Aa aa
<------ !!LESS FIT!! ------>
Is there an internal equilibrium? Yes, our formula for p* shows IT is again in the range 0 to 1; but this time, the equilibrium only remains if the population starts at exactly that frequency. Whatsoever slight perturbation, and it will diverge away from the equilibrium, and eventually run along to fixation at p=0 or p=1. The equilibrium is hither unstable , in which case the only stable equlibria are p=0 and p=1. This is quite an important case; because it also represents hybrid inviability ; this is common when we cross different species, and is possibly an central cause of speciation.
You could try making s negative, and t positive or frailty-versa. The same p* is still an balance, but it isn�t a display case of heterozygous advantage surgery disadvantage, it is a case alike one we have dealt with already. Where is the "non-trivial" equilibrium instantly? Calculate the relative fitnesses w AA , w Aa , w aa : what kinda selection is this? Is the "internal" equilibrium sensible? You could try retired simulating these different fitnesses, heterozygous disfavour, heterozygous advantage, victimization real values in self-generated selection simulations, if you precious.
Now let�s try a real exemplar, in humans: malaria resistance.
ESTIMATING SELECTION
The data is electrophoretic forms of haemoglobin: observations of beta-haemoglobin S (sickle-cell) and A (normal) genotypes in a malaria-infested region of West Africa (simplified from Cavalli Sforza &adenylic acid; Bodmer 1971; available in Science Lbrary: Eyeshot 2007 Teaching Appeal aside leaving to eUCLid; practice Keyword, Basic Hunting, All Fields: 2007). We have seen that one of the assumptions of Hardy-Weinberg equilibrium is that there is no selection. If genotypic ratios deviate from Hardy-Weinberg, we may shady selection provided we terminate rule out inbreeding, migration or another factors. Here we use a![]() test to find whether there is manifest for deviation from Thomas Hardy-Weinberg:
test to find whether there is manifest for deviation from Thomas Hardy-Weinberg:
Examination whether data conforms to Hardy-Steven Weinberg ratios:
Table of genotype oftenness calculations:
Genotype AA Arsenic SS Add togetherO(bserved number) 25,374 5,482 67 30,923Expected fraction 0.8266 0.1651 0.0082 0.999*E(xpected number) (25,561.98) (5,106.03) (254.98) 30,922.99*
Calculations of gene frequency and![]() test:
test:
Gene frequency ![]()
Assuming Hardy-Weinberg, the likely genetic constitution frequencies and expected numbers can right away be calculated - see table above. (*Calculator notes)
Chi-foursquare screen:![]() .
.
Although there are 3 classes of genotypes, we lose degrees of freedom for any estimates we make from the data. We lose 1 because we obtain the total from the information, and 1 because we estimate the gene frequency from the data, leaving 3 - 2 =1 degree of freedom in this slip.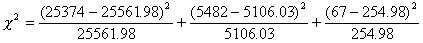
= 1.4 + 27.7 + 138.6 = 167.7
Look for this value of![]() in your
in your![]() tables, under 1 degree of freedom. You find that
tables, under 1 degree of freedom. You find that![]() =167.7 greatly exceeds the value for P=0.001, which is
=167.7 greatly exceeds the value for P=0.001, which is![]() =10.83. Therefore we can enounce that the chance of getting a
=10.83. Therefore we can enounce that the chance of getting a![]() this big in a large numeral of trials if the "null hypothesis" (i.e. Hardy-Steven Weinberg ratios) were true is more less than one in a thousand . In other words, at that place is very strong evidence for a deviation from Hardy-Weinberg -- we turn away the null hypothesis.
this big in a large numeral of trials if the "null hypothesis" (i.e. Hardy-Steven Weinberg ratios) were true is more less than one in a thousand . In other words, at that place is very strong evidence for a deviation from Hardy-Weinberg -- we turn away the null hypothesis.
We usually enunciat all this more briefly: "there is a significant deviation from Hardy-Steven Weinberg, P<0.001".
Estimating selection coefficients:
If we know that the population is non inbreeding, and we suspect excerpt against homozygotes; we can estimate the selection supported on the data we have just analysed:
Genetic constitution AA AS SS Work down fitnesses, O/E 0.99 1.07 0.26 now divide these through by by 1.07 to obtain .. Relative fitnesses W AA W Equally W SS Thence the values of the selection coefficients are estimated as: s = 0.08, t = 0.76. (Check the resolve?)Values of fitnesses rel. to AS 0.92 1.00 0.24Our selection model 1 - s 1 1 - t
TAKE HOME POINTS
- Thither is more than inheritable variation in nature
- Polymorphisms within populations be explained in a variety of ways:
- Survival of the fittest straight favours polymorphism
- heterozygote advantage (done now)
- frequency-dependent selection
- A symmetry of evolutionary forces results in polymorphic equlibrium
- a balance between mutation and selection
- a balance betwixt mutation and genetic rove (neutral evolution)
- a balance betwixt spatially varying selection and migration
- If we have information about fitnesses for heterozygote advantage at a unique locus with two alleles, we can predict the polymorphic vestibular sense frequency p*
- In cases (such as in sickle-mobile phone haemoglobin alleles) where heterozygote advantage is suspected, we can use deviations from Hardy-Weinberg in populations to reckon selection pressures
FUTUYMA, Disk jockey 1998. Evolutionary Biology. Chapter 9 (pp. 231-247); Chapter 13 (pp. 376, 381-390).
Skill Lbrary: View 2007 Teaching Collection by going to eUCLid; use Keyword, Basic Search, All Fields: 2007
Back to BIOL 2007 TIMETABLE
what is the importance of neutral variation in evolution
Source: https://www.ucl.ac.uk/~ucbhdjm/courses/b242/MaintVar/MaintVar.html
Posting Komentar untuk "what is the importance of neutral variation in evolution"